 Elektronik und Co.de
Elektronik und Co.de
Wir schreiben über unsere Projekte
Grundlagen der Operationsverstärker ✏ 🔖 Operationsverstärker 📅 23. Juni 2021
Funktion von OPVs und Verstärkerschaltungen
Ein Operationsvertärker ist ein elektronisches Bauteil mit zwei Eingängen (positivem und negativem) sowie einem Ausgang.

Im folgenden wird nur ein idealer Operationsverstärker behandelt.
Ein Operationsverstärker hat nur ein Ziel und befolgt dabei einige Regeln:
- Ziel: Beide Eingangsspannungen sollen gleich sein $U_{E+} = U_{E-}$
- Ist die Spannung am +Eingang ($U_{E+}$) höher als am -Eingang ($U_{E-}$), so erhöht er die Ausgangsspannung ($U_{out}$)
- Ist die Spannung am -Eingang ($U_{E-}$) höher als am +Eingang ($U_{E+}$), so verringert er die Ausgangsspannung ($U_{out}$)
- In die Eingänge fließt kein Strom
Spannungsfolger / Impedanzwandler
Anhand der oben gegebenen Regeln lässt sich einfach die erste Schaltung ableiten. Der Spannungsfolger.
Verbinden wir den Ausgang mit dem -Eingang (auch negatives Feedback genannt), so erhalten wir einen einfachen Verstärker. Da der Operationsverstärker nach den oben genannten Regeln versucht die Eingangsspannungen gleich zu halten ergibt sich, dass die Ausgangsspannung (= Spannung am - Eingang) gleich der Spannung am +Eingang entsprechen muss.
\[U_{out} = U_{E-} = U_{E+} = U_{in}\]Der Vorteil dieser Schaltung ist, dass am Ausgang auch ein Strom gezogen werden kann, ohne die Eingangsspannung zu belasten. Die Impedanz, also der vom “Abnehmer” erkennbare Innenwiderstand der Quelle, wird also angepasst.
Die Spannungsverstärkung $h$ und der Eingangswiderstand dieser Schaltung ergibt sich daher durch:
\[h = \frac{U_{out}}{U_{in}} = 1\]Da die Quelle $U_{in}$ ist nur an einen Eingang des Operationsverstärkers angeschlossen und wird somit nicht belastet.
\[R_{in} = \infty\]Nichtinvertierender Verstärker
Wird eine Verstärkung von $h > 1$ benötigt, so kann die die Ausgangsspannung über einen Spannungsteiler reduziert werden, bevor sie an den -Eingang zurückgeführt wird:
Wie geplant, steht die Ausgangsspannung in Relation zur Eingangsspannung und dem Verhältnis der beiden Widerstände:
\[U_{in} = U_{E+} = U_{E-} = U_{out} \cdot \frac{R_2}{R_1+R_2} \Rightarrow U_{out} = U_{in} \cdot \frac{R_1+R_2}{R_2} = U_{in} \cdot (\frac{R_1}{R_2} + 1)\]Durch Ableiten erhalten wir die Verstärkung für diese Verschaltung.
\[h = \frac{U_{out}}{U_{in}} = \frac{R_1+R_2}{R_2} = \frac{R_1}{R_2} + 1\]Anhand der Formel lässt sich erkennen, dass die Verstärkung niemals geringer als 1 sein kann für diese Schaltung. Auch hier wird erreicht, dass die Quelle nicht belastet wird, die Last am Ausgang somit einen höheren Strom ziehen kann.
Wie beim Impedanzwandler ist die Quelle nur an den Operationsverstärker angeschlossen und somit nicht belastet.
\[R_{in} = \infty\]Nichtinvertierender Verstärker mit Verstärkung < 1
Um eine Verstärkung des Signals zu erreichen, die im Bereich von $0 < h < 1$ liegt, kann die Spannung zuvor über einen Spannungsteiler reduziert und anschließend mit einem Impedanzwandler verstärkt werden.
Hierfür ergibt sich dann die Formel:
\[U_{in,op} = U_{in} \cdot \frac{R2}{R1+R2} \Rightarrow U_{out} = U_{in} \cdot \frac{R2}{R1+R2}\]Diese Schaltung belastet dann über den Spannungsteiler am Eingang die Quelle, jedoch unabhängig von der Last ist die Belastung der Quelle konstant.
Die Verstärkung lässt sich auch hier aus der Ableitung der Übertragung bestimmen
\[h = \frac{U_{out}}{U_{in}} = \frac{R2}{R1+R2}\]Negativ an dieser Lösung jedoch ist, dass der Spannungsteiler am Eingang die Spannungsquelle belastet und somit das Signal verfälscht:
\[R_{in} = R_1 + R_2\]invertierender Verstärker
Soll in einer Anwendung eine negative Verstärkung ($h < 0$) erreicht werden, so kann der Operationsverstärker als invertierender Verstärker beschaltet werden.
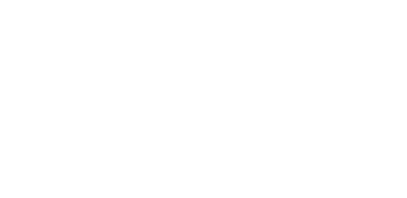
Gemäß der Vorgabe, dass die Eingangsspannungen gleich sein sollen, können wir annehmen dass die Spannung zwischen $R_1$ und $R_2$ 0V beträgt. Dieser Punkt wird gelegentlich auch als “virtuelle Masse” bezeichnet, da sie immer die Gleiche Spannung wie Masse führt, aber keine wirkliche Masse ist. Vereinfacht ergibt sich daraus das nachfolgende Schaubild:
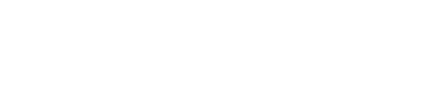
Anhand dieser Vereinfachung ist ersichtlich, dass $U_{in}$ ($= U_{R1}$) mit $R_1$ einen Strom verursacht. Damit diese Schaltung schlüssig funktioniert, muss dieser Strom durch $R_2$ wieder abfließen.
\[I = \frac{U_{in}}{R_1} = -\frac{U_{out}}{R_2} \Rightarrow U_{out} = U_{in} \cdot \frac{R_2}{R_1}\]Die Verstärkung ist auch in diesem Fall gegeben durch die Werte der Widerstände.
\[h = \frac{U_{out}}{U_{in}} = -\frac{R_2}{R_1}\]Die herangehensweise über den Strom zeigt bereits, dass von der Spannungsquelle ein Strom fließen muss, die Quelle somit also belastet ist. Durch die virtuelle Masse ergibt sich der Eingangswiderstand:
\[R_{in} = R_1\]Addierer
Aufbauend auf dem invertierenden Verstärker besteht die Möglichkeit, mehrere Widerstände am Eingang anzuschließen, um mehrere Eingangsströme zusammenzuführen.
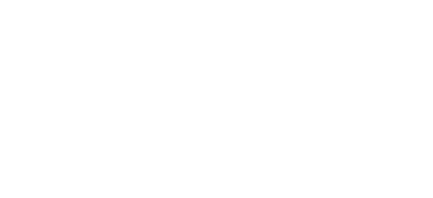
Auch diese Schaltung lässt sich wie der invertierende Verstärker zur Analyse vereinfacht darstellen:
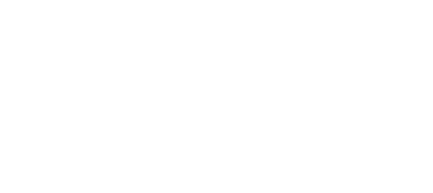
Die Schaltung erfüllt somit die Funktion eines invertierenden Addierers. Da die Schaltung mehrere Eingänge (hier zwei, mehr Eingänge sind durch weiteres Hinzufügen von Widerständen möglich) verfügt, müssen wir die Verstärkung der Eingänge einzeln betrachten:
\[h_{in1} = -\frac{R_3}{R_1}, h_{in2} = -\frac{R_3}{R_2}, ...\]Der Eingangswiderstand für jeden Eingang ist gegeben wie beim invertierenden Verstärker:
\[R_{in1} = R_1, R_{in2} = R_2, ...\]Subtrahierer
Durch kombination des invertierenden sowie nichtinvertierenden Verstärkers lässt sich auch ein Subtrahierer realisieren.

Die Funktion des Operationsverstärkers ist, wie zu erwarten, die Kombination aus beiden vorhergehenden Schaltungen:
\[U_{out} = U_{in2} \cdot \frac{R4}{R2+R4} - U_{in1} \cdot \frac{R_3}{R_1}\]Weitere Verschaltungen
In diesem Beitrag wurden nur Schaltungen mit negativem Feedback, also reine Verstärker, behandelt.
Es ist auch möglich ein positives Feedback, eine Rückführung des Signals auf den +Eingang, zu geben, wodurch ein Schmitt-Trigger-Verhalten eingeführt wird.
Ebenso können frequenzabhängige Bauteile wie Spulen und Kondensatoren eingesetzt werden, um Integratoren und Differenzierer zu erhalten oder ein Filterverhalten zu erreichen.
Diese werden in einem späteren Beitrag behandelt.
Noch Fragen? $\Rightarrow$ Schreibt ein Kommentar oder schickt mir einfach eine Nachricht. ;)