Binäre Zahlenysteme ✏ Kevin 🔖 Zahlen 📅 9. Januar 2022

Einer- und Zweierkomplement, Greycode

Binäre Zahlensysteme sind heute die verbreitetsten Systeme, da jeder Computer binär arbeitet. Sie unterscheiden sich nur wenig von dem dezimalen System, das wir im Alltag benutzen, wirken aber auf den ersten Moment etwas fremd.

Wiederholung Dezimalsystem

In unserem Dezimalsystem bezieht sich alles auf die Basis 10. So kann jede Ziffer einen beliebigen Wert $d \in {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}$ annehmen (10 Möglichkeiten). Die Wertigkeit der Zahl ist zudem abhängig davon, an welcher Stelle sie steht:

\[\begin{array} {c|c|c|c|c|c|c|c} ... & Tausender & Hunderter & Zehner & Einer & Komma & Zehntel & Hundertstel & ... \\ ... & \cdot 10^3 = \cdot 1000 & \cdot 10^2 = \cdot 100 & \cdot 10^1 = \cdot 10 & \cdot 10^0 = \cdot 1 & & \cdot 10^{-1} = \cdot 0.1 & \cdot 10^{-2}= \cdot 0.01 & ... \\ \end{array}\]

Die dezimale Zahl $172_d$ bedeutet also

\[172_d = 1 \cdot 10^2 + 7 \cdot 10^1 + 2 \cdot 10^0\]

Dieses Schema ist anwendbar für Zahlensysteme mit beliebiger Basis sowie beliebig lange Zahlen.

Positive binäre Zahlen

Ein Computer versteht nur “aus” = 0 und “an” = 1, also ein binäres System mit der Basis $2$. Der Wertebereich eines Bit ist somit $d \in {0, 1}$.

Die Wertigkeit eines Zeichens ist auch hier von der Position definiert:

\[\begin{array} {c|c|c|c|c|c|c|c} ... & \cdot 2^3 = \cdot 8 & \cdot 2^2 = \cdot 4 & \cdot 2^1 = \cdot 2 & \cdot 2^0 = \cdot 1 & Komma & \cdot 2^{-1} = \cdot 0.5 & \cdot 2^{-2}= \cdot 0.25 & ... \\ \end{array}\]

die Zahl 101010 im Binärsystem ergibt somit:

\[\begin{array} {r l} 101010_b &= 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 \\ &= 1 \cdot 32 + 1 \cdot 8 + 1 \cdot 2 \\ &= 42_d \end{array}\]

Wird die Zahl in einem System mit negativen Zahlen verwendet, so ist eine Positive Zahl an einer führenden 0 zu erkennen wie z.B.

\[42_b = 0101010_{BV} = 0101010_{EK} = 0101010_{ZK}\]

Positive Zahlen sind in allen nachfolgenden Zahlensystemen (Betrag mit Vorzeichen, Einerkomplement und Zweierkomplement) gleich.

Negative Zahlen I: Betrag mit Vorzeichen

Natürlich gibt es auch negative Zahlen. Diese stellen wir im Dezimalsystem durch ein führendes Minus dar, z.B. $-172_d$. Beim händischen Arbeiten ist dies kein Problem, da die Länge der Zahl flexibel ist und es für einen Menschen offensichtlich ist, was das Minus bedeutet. Ein Computer kann das aber leider nicht, also muss definiert werden, wie eine negative Zahl auszusehen hat.

Ein Ansatz ist es, immer das höchstwertigste Bit als Vorzeichen zu benutzen:

\[\begin{array} {c|c|c|c|c|c|c|c} Vorzeichen & ... & \cdot 2^2 = \cdot 4 & \cdot 2^1 = \cdot 2 & \cdot 2^0 = \cdot 1 & Komma & \cdot 2^{-1} = \cdot 0.5 & \cdot 2^{-2}= \cdot 0.25 & ... \\ \end{array}\]

Die vorhin verwendete Zahl von $101010_b$ benötigt somit eine führende Ziffer, um das Vorzeichen anzugeben:

\[\begin{array} {r l} 101010_b &= 0101010_{BV} = 42_d \\ -101010_b &= 1101010_{BV} = -42_d \end{array}\]

Der Nachteil dieser Schreibweise ist, dass das Rechnen mit diesem System sehr kompliziert ist und dass es eine positive und eine negative Null gibt, wir also unseren Speicher nicht optimal benutzen:

\[\begin{array} {r l} 0 0_{BV} &= +0_b \\ 1 0_{BV} &= -0_b \end{array}\]

Rechnen auf einem binären Niveau ist hier relativ kompliziert und wird daher nicht gemacht,

Negative Zahlen II: Einerkomplement

Sehr ähnlich zum Betrag mit Vorzeichen gibt es das Einerkomplement. Auch hier wird die negative Zahl durch eine führende 1 angezeigt. Der Wechsel zwischen der Negativen und der Positiven Zahl erfolgt hier durch das invertieren aller Ziffern (=Bits).

\[-42_d = -00101010_b = \sim00101010_b = 11010101_{EK}\]

Randnotiz: Das Tilde-Symbol $\sim$ bedeutet, dass alle Bits einzeln invertiert werden sollen. Dieses Symbol wird auch in vielen Programmiersprachen so verwendet.

Auch hier gibt sich aber das Problem, dass es die Null doppelt gibt:

\[- 00000000_{EK} = 11111111_{EK}\]

Bei Additionen gibt es jedoch ein Problem, dass im Falle eines Überlaufs $Ü$ die Werte nicht stimmen. Um das zu berücksichtigen, muss der Betrag auf das Endergebnis noch aufaddiert werden:

\[-42_d - 42_d = 11010101_{EK} + 11010101_{EK} = 1_{Ü} 10101010_{EK} = 1_{Ü} + 10101010_{EK} = 10101011_{EK} = -01010100_{EK} = - 84_d\]

Negative Zahlen III: Zweierkomplement

Um den Speicher möglichst voll zu nutzen, wurde das Einerkomplement etwas ergänzt:
Eine negative Zahl ergibt sich durch invertieren aller Bits und anschließendes Addieren einer 1.

\[-42_d = -00101010_b = \sim(00101010_b)+1_b = 11010110_{ZK}\]

Diese Vorgehensweise verhindert das doppelte Belegen der Null:

\[-0_d = -00000000_b = \sim(00000000_b)+1_b = 11111111_b+1_b = 00000000_{ZK}\]

Bei einer Addition ist hier nichts weiter zu beachten:

\[-42_d + 42_d = 00101010_{ZK} + 11010110_{ZK} = 1 00000000_{ZK}\]

Der Überlauf kann hier verwendet werden um zu prüfen, ob der errechnete Wert möglicherweise zu groß ist für den Speicherbereich. Die nachfolgende Tabelle zeigt die erwarteten Überträge, sofern kein Überlauf vorliegt unter Abhängigkeit der Vorzeichen der addierten Zahlen:

\[\begin{array} {r|c|c} & Negativ & Positiv \\ \hline Negativ & 1 & 1 \\ Positiv & 1 & 0 \end{array}\]

Greycode

Der Grey-Code hat für das Rechnen keinen Vorteil, wird aber oft zur Positionsbestimmung eingesetzt. Ziel beim Grey-Code ist, dass sich für jeden Schritt immer nur ein bit ändert - also eine Position zwischen zwei Werten eindeutig ist. Wie der Grey-Code aufgebaut ist und wie man ihn um ein Bit erweitert, ist nachfolgend abgebildet.

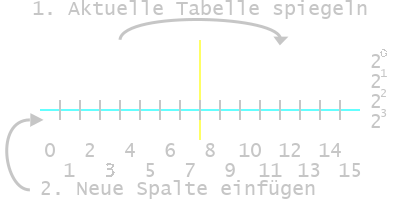
Weiße Felder repräsentieren eine 1, graue/leere Bereiche eine 0.