Einfache Diodenschaltungen ✏ Kevin 🔖 Dioden 📅 29. August 2020

Analyse von Schaltungen mit Dioden an DC

Da ich in der letzten Zeit häufiger erklären durfte, wie denn Schaltungen mit Dioden funktionieren habe ich mich entschieden das hier zusammenzufassen. Dieser Artikel behandelt ausschließlich idealisierte Schaltungen.

Rechenmodelle von Dioden

Für die Berechnung von Dioden-Schaltungen werden in der Regel drei verschiedene Dioden eingesetzt, je nachdem wie genau die Berechnung sein muss. Die Betrachtungen unterscheiden sich eigentlich nur in der angenommenen Schwellspannung in Durchlassrichtung:

Typ	Vorwärtsspannung
Ideale Diode	$U_D = 0V$
Vereinfachte Diode	$U_D = 0.6V$
Reale Diode1	$U_D = \ln{\left( \frac{I_D}{I_S}-1 \right)} \cdot \frac{nk_BT}{q}$

Eine alternative Darstellung von Dioden lässt sich über eine Ideale Diode mit einer idealen Spannungsquelle realisieren.

Diese Art der Darstellung ist mir bisher in der Praxis noch nie in die Hände gekommen, aber für theoretische Arbeiten (oder für Klausuren und andere Abfragen) ist diese Darstellung nicht selten.

Bei der Analyse einer Schaltung ist es am Einfachsten, die Betrachtung immer bei 0V zu beginnen. Für jede Diode wird dann eine Formel in der Form $U_{in}(U_{D_n})$ aufgestellt, ab welcher Eingangsspannung die Diode leitet. Gibt man dieser als Parameter die Schwellspannung der Diode an erhält man somit die nötige Eingangsspannung.

Mehrere Dioden in Reihe könnt ihr einfach zu einer Diode mit entsprechend der Summe aller Vorwärtsspannungen zusammenfassen - das macht das Arbeiten oft einfacher.

Einfache Schaltungen mit Dioden

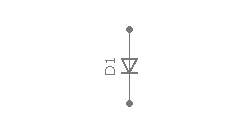
Die einfachste Didenschaltung ist eine Reihenschaltung aus einer Diode und einem Widerstand.

In Sperrrichtung wird - unabhängig davon wie hoch $U_{in}$ ist, die volle Spannung an der Diode abfallen, da diese keinen Stromfluss zulässt und somit nach Ohm’schem Gesetz $U=R \cdot I$ mit $I=0$ auch $U=0$ keine Spannung am Widerstand abfallen kann.

In Durchlassrichtung fällt erstmal alle Spannung an der Diode ab bis diese die ihre benötigte Vorwärtsspannung erreicht. Dieses Verhalten lässt sich mit einer unterbrechung des Stromkreises vergleichen. Die Spannung der idealen/vereinfachten Diode wird niemals eine Spannung höher als ihre Schwellspannung in Durchlassrichtung haben!

Nun gilt es die entsprechenden Spannungsbereiche zu betrachten:

Für $U_{in} \leq U_S$ gilt

$U_D = U_{in}$

Für $U_{in} \geq U_S$ gilt

$U_D = U_S$

Für den Strom gilt in dieser Schaltung immer

$I = \frac{U_{in} - U_D}{R}$

Die übrige Spannung welche die Diode sich nicht nimmt, fällt entsprechend am Widerstand ab, welcher zudem den Strom begrenzt. Würde die Diode ohne Widerstand betrieben werden, würde rechnerisch ein unendlich großer Strom fließen, da die Diode in der Theorie keinen Ohm’schen Widerstand hat.

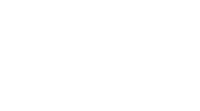
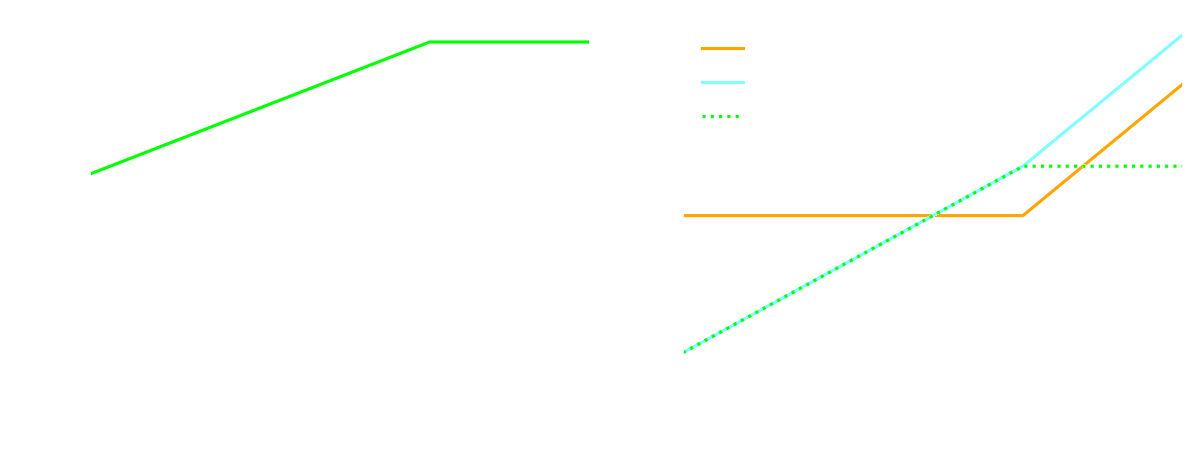
Für diese Schaltung ergibt sich für eine idealisierte Diode mit $U_S = 0.6V$ ergibt sich die folgende Kennlinie.

Weitere Aufgabe mit Dioden

Betrachten wir nun folgende, etwas komplexere Aufgabe mit zwei Widerständen und einer Diode:

Für kleine sowie negative Spannungen sperrt die Diode kann ignoriert werden. Dies gilt, bis die Spannung über der Diode, hier $U_{out}$ die Schwellspannung $U_S$ erreicht.

Die Grenze des Bereichs in dem die Diode sperrt ergibt sich entsprechend:

\[U_{out} = U_S = U_{in} \cdot \frac{R_2}{R_1+R_2}\]

Durch umstellen und einsetzen erhalten wir:

\[U_S \cdot \frac{R_1+R_2}{R_2} = 0.6V \cdot \frac{2k\Omega+1k\Omega}{1k\Omega} = 0.6V \cdot 3 = 1.8V = U_{in}\]

Überschreiten wir diese Stufe, begrenzt die Diode die Spannung über $R_1$ auf $U_S$ und wie in der vorherigen Schaltung nimmt der Vorwiderstand, hier $R_1$ die restliche Spannung.

Entsprechend erhalten wir für diese Aufgabe:

Für $U_{in} \leq 1.8V$ gilt

$U_{out} = U_{in} \cdot \frac{R_2}{R_1+R_2}$

$I = \frac{U_{in}}{R_1+R_2}$

$I_{R_1} = I_{R_2} = I$

$I_{D_1} = 0$

Für $U_{in} \geq 1.8V$ gilt

$U_D = U_S = 0.6V$

$I = \frac{U_{in}}{R_1+R_2}$

$I_{R_1} = \frac{U_{in}-U_S}{R_1} = \frac{U_{in} - 0.6V}{R_1}$

$I_{R_2} = \frac{U_S}{R_2} = \frac{0.6V}{R_2} = 0.6mA$

$I_{D} = I_{R_1} - I_{R_2} = I_{R_1} - 0.6mA$

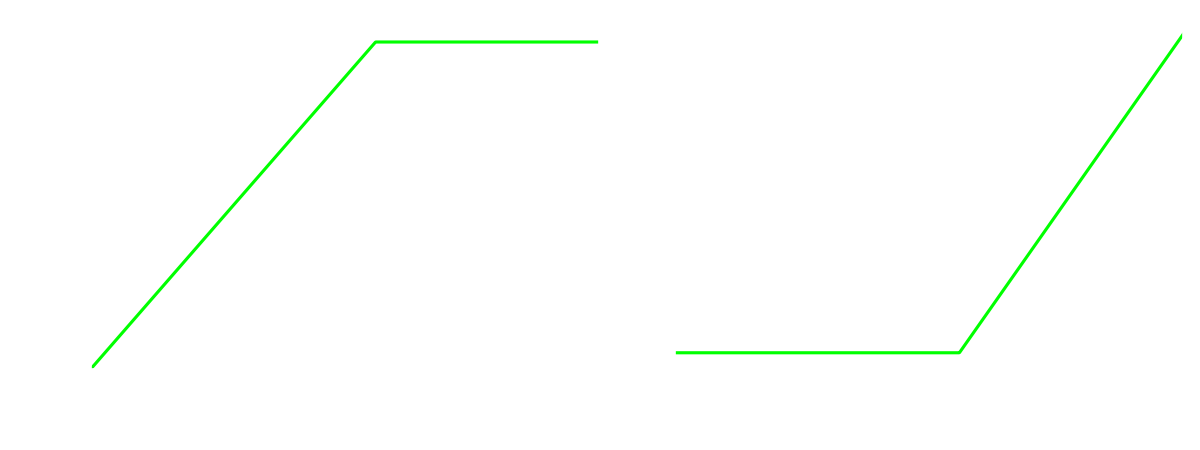
Auch das Verhalten lässt sich grafisch darstellen wie nachfolgend zu sehen. Außerhalb des Bereichs gibt es keine Knickpunkte mehr, die Linien können also über das Diagramm hinaus ins Unendliche als Gerade fortgesetzt werden.

Für Studenten habe ich hier aus meiner vergangenen Elektrotechnik-Klausur noch einen Spickzettel, den ich damals in der Klausur verwendet habe. Vielleicht hat ja der eine oder andere Besucher hier eine Verwendung dafür. Danke auch an Lee-Ann für die fleißige Unterstützung und die Handzeichnungen.

Wenn Ihr noch Verbesserungen oder Ergänzungen habt schickt sie mir gerne zu oder schreibt sie unten in die Kommentare. :)

Anhang:

• Klausur-Spicker (Ursprüngliche Version)
• Klausur-Spicker (Mit einigen Änderunen)